THE CHALLENGE
Optimizing solutions to complex problems with multiple constraints is difficult to achieve. Analytical and practical evidence indicates the advantage of quantum computing solutions over classical alternatives. Quantum-based heuristics relying on the variational quantum eigensolver (VQE) and the quantum approximate optimization algorithm (QAOA) have been shown to generate high-quality solutions to hard combinatorial problems, yet incorporating constraints to such problems has been elusive.
OUR SOLUTION
Quantum heuristic offers new method for optimizing constrained computational problems. This quantum-based heuristic is designed to solve stochastic binary quadratically constrained quadratic programs (QCQP). When identifying the strength of quantum circuits to efficiently generate samples from probability distributions that are otherwise hard to sample, the variational quantum circuit is trained to generate binary-valued vectors to approximately solve stochastic programs. The method builds upon dual decomposition and entails solving a sequence of judiciously modified standard VQE tasks. Tests on several synthetic problem instances using a quantum simulator corroborate the near-optimality and feasibility of the method and its potential to generate feasible solutions for the deterministic QCQP.
This first comprehensive attempt to deal with deterministic and stochastic combinatorial problems with constraints using a quantum computer could have significant impact toward dealing with a diverse gamut of combinatorial problems in operations research, wireless communications, and machine learning.
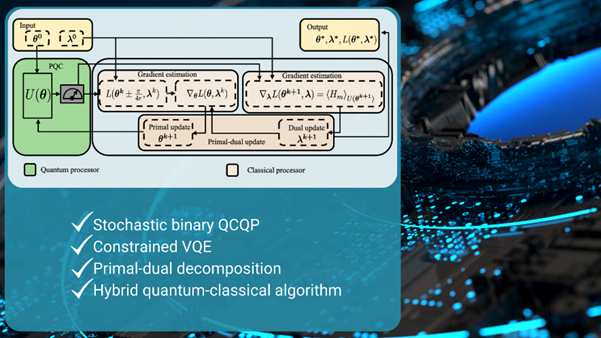
Figure: Quantum-based heuristic solves stochastic binary quadratically constrained quadratic programs (QCQP)
Advantages
- Flexible: Permits a broad class of constraints, such as quadratic inequality
- Enabling: Builds on dual and primal-dual decompositions along with the stochastic variants applied to the quantum setup
- Innovative: Sets the foundation for further developments toward constrained discrete optimization
Potential Applications:
Applicable for solving large-scale stochastic mixed-integer problems with constraints that appear in the following instances:
- Operation of electric power systems
- Optimal resource allocation in wireless networking
- Optimal scheduling tasks in online advertising space allocation, airplane management, delivery routes, and stock trading
- Logistics
- Supply chain optimization
- Distribution network optimization